Glimpse
In thermodynamics, the macroscopic variables, like temperature and pressure and volume dealing. The main laws of thermodynamics are expressed in terms such Kmythayy. Nothing about that matter is made of atoms, do not talk. However, statistical mechanics, the science dealing with the same Hythay of thermodynamics, it argues that the existence of atoms as previously assumed. The main laws of statistical mechanics pro Mkanykand rules that are used in approximately log-forming atoms.
History
ryKinetic Theory by Robert Boyle (Rabert Boyle) (1627 - 1691), Daniel Bernoulli (1700-1782), James Joule (1818-1889), Krvnyg (1822-1874), Rudolf Klavsyvs (1822-1888) and Clerk Maxwell (1831 - 1879) and others has come into being. The kinetic theory of gases, apply only in the case, because the Interactions between atoms in gases than in liquids Mtghyrtrnd. This math problem is much easier.
The laws of statistical mechanics can be at another level, using methods that are used Svrytr and abstract methods of kinetic theory. This approach by J. Willard Gibbs (J.willard Gibbs) and Mani Bvltz Ludwig (Ludwig Boltz manni) (1844 - 1906) and others has evolved, called statistical mechanics, the kinetic theory as a minor branch of the takes. Using this method we can obtain the laws of thermodynamics. Thus it is clear that thermodynamics is a branch of mechanics.
img / daneshnameh_up / b / bb / Brownian.gif
Pressure is calculated based on kinetic theory
An ideal gas pressure are calculated using the kinetic theory. To simplify this, the gas in a cube-shaped container with perfectly elastic walls consider. Assume L is the length of each side of the cube. Surfaces perpendicular to the X axis is the area of each e2. Called A1 and A2. Consider that V is the molecular velocity. V velocity components Vx and Vy and Vz can be decomposed along the edges.
If this particle will collide with the A1 at the rate of return component of X is reversed. Hence the effect of Vy and Vy are the components of the momentum variables will include:
m Vx - m Vx) = 2 m Vx -) = initial momentum - the momentum
That is perpendicular to the A1. So the momentum is given by e to A1 will be equal to m Vx2 because the total momentum is Paysth.
Time required to traverse the cube will be Vx / L. Y component of particle velocity is reversed again in A2 to A1 returns. The case does not conflict with the assumption that the sweep period will be equal to 2 e Vx. So that the transfer of momentum from the particle track is A1:
mVx2 / e = Vx/2e. 2 mVx, to obtain the total force exerted on the surface of A1, the momentum transfer songs from all the gas molecules is given to the A1.
(P = M / e (Vx12 + Vx22 + Vx32
P = 1/2eV2
img/daneshnameh_up/a/a3/damping.gif
Interpretation of temperature on the kinetic theory
According to the formula RT 2/3 = 1/2 MV2 the total energy transferred per mole of molecules of an ideal gas, is proportional to temperature.Or can the above equation as the definition of temperature based on the kinetic theory or Mykrvskvbyk considered. The concept gives us insight into both the gas temperature. The temperature of a gas is related to the total kinetic energy transferred to the center of mass of gas is measured. Kinetic energy to move the center of mass of gas is related to gas temperature.
Katvrhay move as part of the statistical definition of an ideal gas is considered. V2 can be calculated on this basis. Katvrhay in a distribution of molecular speeds, will be the center of mass at rest. So we must apply the reference frame in which the gas center of mass is at rest. In other contexts, the speed of each of the molecules to U (velocity in the center of mass frame) is the velocity in the center of mass. Other movements Ktrhay then be derived for different values of V2. The gas temperature inside a container in a moving train increases. We know that M V2 1/2 the average kinetic energy per molecule is transitional. This quantity at a certain temperature, which in this case is zero degrees Celsius, has the same value for all gases. We conclude that the temperature T, the root mean square speed of gas molecules is equal to two shots at the root of their squares.
T = 2/3k m1 V12 / 2 = 2/3k m2 V22 / 2
img/daneshnameh_up/b/b3/adia.gif
The mean free distance
Continuous in space collisions, the molecules of the gas moves with constant speed along a straight line. The average distance is called the mean free distance between the continuous encounters. If molecules were to form a point, I did not collide. And the mean free distance was infinite. Molecules and thus encounters occur, but are not the point.It was a zero mean free distance.
The mean free distance depends on the size and number of molecules per unit volume of the unit. And the diameter d and the gas molecules are spherical in this section will deal with лd2.
2d molecular diameter to consider that the gas velocity V of the point particle exchange moves. T for this molecule in the cylindrical cross-section and length лd2 the Myrvbd Vt. If nv is the number of molecules per unit volume of the cylinder (лd2 Vt) nv the particle. The mean free distance, L, the average distance between two collisions is therefore continuous, L, is the total distance that the molecules in Mypymayd t. (Vt) divided by the number of encounters during which you will perform. Namely:
I = Vt/πd2nv = 1 / √ 2πnd2
I = 1 / √ 2πnd2
This average is based on a video in which a molecule will collide with stationary targets. In fact, the number of collisions of molecules with temperatures moving into the temperature is higher than this value.
Distribution of molecular speeds
The Root Mean Squared velocity of gas molecules, but the individual molecules is very broad speed range. Mnhnyay of molecular gas velocities so that for each there is a temperature-dependent. If the speeds are all identical molecules of a gas can not long survive this situation. The molecular speeds due to collisions will change.The most probable velocity distribution in a large number of gas molecules, Maxwell Klvk solved first. He said the law provided that the N molecules in a sample of gas is not covered:
N (V) = 4πN (m/2πKt) 3/2V2e-mv2/2kt
In this equation, N (V) dV is the number of molecules between V and V +3 v is velocity, T the absolute temperature, K Boltzmann constant, m is the mass of each molecule. The total number of gas molecules (N), with the sums (ie integration) number in each speed range from zero to infinity differential is achieved. Unit (N (V cm per second can be for such molecules.
N = ∫ ∞ 0N (V) dv
Distribution of molecular speeds in liquids
Distribution of molecular speeds in a fluid-like gas. But some of the liquid molecules (faster ones) can be at temperatures well below the normal boiling point of liquid surface escape. (Ie they evaporate). These are molecules that can appeal only to overcome the surface molecules. And evaporation to escape. Thus the average kinetic energy of the remaining molecules also decreases the fluid temperature is low. It is clear that evaporation is a cooling process.
The real example about the distribution of molecular speeds
So the probability that a hydrogen atmosphere at high altitudes to escape more, until the oxygen and nitrogen. Moon has a thin atmosphere.The evidence, such as krypton and xenon in the atmosphere heavy inert gases are the result of radioactive decay are produced in the past month. Atmospheric pressure at about 10 is equal to atmospheric pressure.
img/daneshnameh_up/7/72/Boltzman.gif
Maxwell distribution
Maxwell distribution of molecular speeds achieved in 1859 AD.Many individuals do this quickly improved techniques. Then in 1955 a very detailed review of empirical confirmation of this law (in the case of gas molecules by Miller (Miller) and I (Kusch) were from Columbia University.
Toys used in these two series of experiments, some thallium in the furnace walls and furnace had a uniform temperature of 80 ± 4K to O were heated. The thallium vapor temperature and pressure of 3.2x10-3 mm Hg, oven fills.For a given angular velocity of cylinder (W) are the only molecules with velocity V can clear the tracks pass through without hitting the wall. Velocity V can be obtained from the following relationship:
V = LW / q and L / V = φ / W = time of molecules through the slot
φ: angular shift between the input and output is a diagonal slot. Is a rapidly rotating cylinder switch, speed selected angular speed (controlled) W is proportional.
Maxwell velocity distribution of defects with the kinetic theory
Although the Maxwell velocity distribution for gas in normal conditions is consistent with observations very well. But Chgalyhay above, the basic assumptions of classical kinetic theory is not true. This consistency is also seen. In these conditions the velocity distributions based on the principles of quantum mechanics, namely the distribution of Fermi - Dirac (Fermi Dirac) Bose - Einstein (Bose Einstein) was used. The quantum distributions in the classical (low density) are in close agreement with the Maxwell distribution where classical distribution fails to be compatible with experimental results. So there are limits on the use of Maxwell distribution. As in any such theory
نظریه جنبشی گازها
قوانین مکانیک را میتوان بطور آماری در دو سطح مختلف به مجموعهای از اتمها اعمال کرد در سطحی که نظریه جنبشی گازها نامیده میشود. به طریقی کم و بیش فیزیکی و با استفاده از روشهای نسبتا ساده میانگین گیری ریاضی ، عمل میکنیم. برای فهم نظریه جنبشی گاز را در فشار ، دما ، گرمای ویژه و انرژی داخلی این روش را که در سطح بکار برده میشود.
نگاه اجمالی
در ترمودینامیک فقط با متغیرهای ماکروسکوپیک ، مانند فشار و دما و حجم سر و کار داریم. قوانین اصلی ترمودینامیکها بر حسب چنین کمیتهایی بیان میشوند. ابدا درباره این امر که ماده از اتمها ساخته شده است صحبتی نمیکنند. لیکن مکانیک آماری ، که با همان حیطهای از علم سر و کار دارد که ترمودینامیک از آن بحث میکند و وجود اتمها را از پیش مفروض میداند. قوانین اصلی مکانیک آماری حامی قوانین مکانیکاند که در حدود اتمهای تشکیل دهنده سیسنم بکار میروند.
تاریخچه
نظریه جنبشی توسط رابرت بویل (Rabert Boyle) (1627 – 1691) ، دانیل بونولی (1700 – 1782) ، جیمز ژول (1818 – 1889) ، کرونیگ (1822 – 1874) ، رودولف کلاوسیوس (1822 – 1888) و کلرک ماکسول ( 1831 – 1879 ) و عدهای دیگر تکوین یافته است. در اینجا نظریه جنبشی را فقط در مورد گازها بکار میبریم، زیرا برهم کنشهای بین اتمها ، در گازها به مراتب متغیرترند تا در مایعات. و این امر مشکلات ریاضی را خیلی آسانتر میکند.
در سطح دیگر میتوان قوانین مکانیک را بطور آماری و با استفاده از روشهایی که صوریتر و انتزاعیتر از روشهای نظریه جنبشی هستند بکار برد. این رهیافت که توسط جی ویلارد گیبس (J.willard Gibbs) و لودویگ بولتز مانی (Ludwig Boltz manni) (1844 – 1906) و دیگران تکامل یافته است، مکانیک آماری نامیده میشود، که نظریه جنبشی را به عنوان یکی از شاخههای فرعی در بر میگیرد. با استفاده از این روشها میتوان قوانین ترمودینامیک را به دست آورد. بدین ترتیب معلوم میشود که ترمودینامیک شاخهای از علم مکانیک است.
محاسبه فشار بر پایه نظریه جنبشی
فشار یک گاز ایدهآل را با استفاده از نظریه جنبشی محاسبه میکنند. برای ساده کردن مطلب ، گازی را در یک ظرف مکعب شکل با دیوارههای کاملا کشسان در نظر میگیریم. فرض میکنیم طول هر ضلع مکعب L باشد. سطحهای عمود بر محور X را که مساحت هر کدام e2 است. A1 و A2 مینامیم. مولکولی را در نظر میگیریم که دارای سرعت V باشد. سرعت V را میتوان در راستای یالهای مولفههای Vx و Vy و Vz تجزیه کرد. اگر این ذره با A1 برخورد کند در بازگشت مولفه X سرعت آن معکوس می شود. این برخورد اثری رو ی مولفه Vy و یا Vy ندارد در نتیجه متغیر اندازه حرکت عبارت خواهد بود :
(m Vx - m Vx) = 2 m Vx - )= اندازه حرکت اولیه – اندازه حرکت نهایی
که بر A1 عمود است. بنابراین اندازه حرکتی e به A1 داده میشود برابر با m Vx2 خواهد بود زیرا اندازه حرکت کل پایسته است.
زمان لازم برای طی کردن مکعب برابر خواهد بود با Vx/L. در A2 دوباره مولفه y سرعت معکوس میشود و ذره به طرف A1 باز میگردد. با این فرض که در این میان برخوردی صورت نمیگیرد مدت رفت و برگشت برابر با 2 e Vx خواهد بود. به طوری که آهنگ انتقال اندازه حرکت از ذره به A1 عبارت است: mVx2/e = Vx/2e . 2 mVx ، برای به دست آوردن نیروی کل وارد بر سطح A1 ، یعنی آهنگ انتقال اندازه حرکتی از طرف تمام مولکولهای گاز به A1 داده میشود.
(P = M/e(Vx12 + Vx22 + Vx32
P = 1/2eV2
تعبیر دما از دیدگاه نظریه جنبشی
با توجه به فرمول RT 2/3 = 1/2 MV2 یعنی انرژی کل انتقال هر مول از مولکولهای یک گاز ایدهآل ، با دما متناسب است. میتوان گفت که این نتیجه با توجه به معادله بالا برای جور در آمدن نظریه جنبشی با معادله حالت یک گاز ایدهآل لازم است. و یا اینکه میتوان معادله بالا را به عنوان تعریفی از دما بر پایه نظریه جنبشی یا بر مبنای میکروسکوبیک در نظر گرفت. هر دو مورد بینشی از مفهوم دمای گاز به ما میدهد. دمای یک گاز مربوط است به انرژی جنبشی انتقال کل نسبت به مرکز جرم گاز اندازه گیری میشود. انرژی جنبشی مربوط به حرکت مرکز جرم گاز ربطی به دمای گاز ندارد.
حرکت کاتورهای را به عنوان بخشی از تعریف آماری یک گاز ایدهآل در نظر گرفت. V2 را بر این اساس میتوان محاسبه کرد. در یک توزیع کاتورهای سرعتهای مولکولی ، مرکز جرم در حال سکون خواهد بود. بنابراین ما باید چارچوب مرجعی را بکار ببریم که در آن مرکز جرم گاز در حال سکون باشد. در چارچوبهای دیگر ، سرعت هر یک از مولکولها به اندازه U (سرعت مرکز جرم در آن چارچوب) از سرعت آنها در چارچوب مرکز جرم بیشتر است. در اینصورت حرکتها دیگر کترهای نخواهد بود و برای V2 مقادیر متفاوتی بدست میآید. پس دمای گاز داخل یک ظرف در یک قطار متحرک افزایش مییابد. میدانیم که M V2 1/2 میانگین انرژی جنبشی انتقالی هر مولکول است. این کمیت در یک دمای معین که در این مورد صفر درجه سلسیوس است، برای همه گازها مقدار تقریبا یکسانی دارد. پس نتیجه میگیریم که در دمای T ، نسبت جذر میانگین مربعی سرعتهای مولکولهای دو گاز مختلف مساوی است با ریشه دمای عکس نسبت به مربعهای آنها.
T=2/3k m1 V12/2= 2/3k m2 V22/2
مسافت آزاد میانگین
در فاصله برخوردهای پیدرپی ، هر مولکول از گاز با سرعت ثابتی در طول یک خط راست حرکت میکند. فاصله متوسط بین این برخوردهای پیدرپی را مسافت آزاد میانگین مینامند. اگر مولکولها به شکل نقطه بودند، اصلا با هم برخورد نمیکردند. و مسافت آزاد میانگین بینهایت میشد. اما مولکولها نقطهای نیستند و بدین جهت برخوردهایی روی میدهد. اگر تعداد مولکولها آنقدر زیاد بود که میتوانستند فضایی را که در اختیار دارند کاملا پر کنند و دیگر جایی برای حرکت انتقالی آنها باقی نمیماند. آن وقت مسافت آزاد میانگین صفر میشد. بنابراین مسافت آزاد میانگین بستگی دارد به اندازه مولکولها و تعداد واحد آنها در واحد حجم. و به قطر d و مولکولهای گاز به صورت کروی هستند در این صورت مقطع برای برخورد برابر با лd2 خواهد بود.
مولکولی با قطر 2d را در نظر میگیریم که با سرعت V در داخل گازی از ذرات نقطهای هم ارز حرکت میکند. این مولکول در مدت t استوانهای با سطح مقطع лd2 و طول Vt را میروبد. اگر nv تعداد مولکولها در واحد حجم باشد استوانه شامل (лd2 Vt ) nv ذره خواهد بود. مسافت آزاد میانگین ، L ، فاصله متوسط بین دو برخورد پیدرپی است بنابراین ، L ، عبارت است از کل مسافتی که مولکول در مدت t میپیماید. (Vt) تقسیم بر تعداد برخوردهایی که در این مدت انجام میدهد. یعنی
I = Vt/πd2nv =1/√2πnd2
I=1/√2πnd2
این میانگین بر مبنای تصویری است که در آن یک مولکول با هدفهای ساکن برخورد میکند. در واقع ، برخوردهای مولکول با هدف دمای متحرک انجام میگیرد در نتیجه تعداد برخورد دما از این مقدار بیشتر است.
توزیع سرعتهای مولکولی
با توجه به سرعت جذر میانگین مربعی مولکولهای گاز ، اما گستره سرعتهای تکتک مولکولها بسیار وسیع است. بطوری که برای هر گازی منحنیای از سرعتها مولکولی وجود دارد که به دما وابسته است. اگر سرعتهای تمام مولکولهای یک گاز یکسان باشند این وضعیت نمیتواند مدت زیاد دوام بیاورد. زیرا سرعتهای مولکولی به علت برخوردها تغییر خواهند کرد. با وجود این انتظار نداریم که سرعت تعداد زیادی از مولکولها بسیار کمتر از Vrms (یعنی نزدیک صفر) یا بسیار بیشتر از Vrms ، زیرا وجود چنین سرعتهایی مستلزم آن است که یک رشته برخوردهایی نامحتمل و موجی صورت بگیرد. مسئله محتملترین توزیع سرعتها در مورد تعداد زیادی از مولکولهای یک گاز را ابتدا کلوک ماکسول حل کرد. قانونی که او ارائه کرد در مورد نمونهای از گاز که N مولکول را شامل میشد چنین است :
N(V)=4πN(m/2πKt)3/2V2e-mv2/2kt
در این معادله N(V)dV تعداد مولکولهایی است که سرعت بین V و V+3v است، T دمای مطلق ، K ثابت بولتزمن ، m جرم هر مولکول است. تعداد کل مولکولهای گاز (N) را ، با جمع کردن (یعنی انتگرالگیری) تعداد موجود در هر بازه دیفرانسیلی سرعت از صفر تا بینهایت به دست میآید. واحد (N(V میتواند مثلا مولکول برا سانتیمتر بر ثانیه باشد.
N =∫∞0N(V)dv
توزیع سرعتهای مولکولی در مایعات
توزیع سرعتهای مولکولی در مایعات شبیه گاز است. اما بعضی از مولکولهای مایع (آنهایی که سریعترند) میتوانند در دماهایی کاملا پایینتر از نقطه جوش عادی از سطح مایع بگریزند. (یعنی تبخیر شوند). فقط این مولکولها هستند که میتوانند بر جاذبه مولکولهای سطح فائق آیند. و در اثر تبخیر فرار کنند. بنابراین انرژی جنبشی میانگین مولکولهای باقیمانده نیز کاهش مییابد در نتیجه دمای مایع پایین میآید. این امر روشن میکند که چرا تبخیر فرایند سرمایشی است.
مثال واقعی در مورد توزیع سرعتهای مولکولی
با توجه به فرمول N(V)= Σ410N(M/2πkT)3/2 توزیع سرعتهای مولکولی هم به جرم مولکول و هم به دما بستگی دارد هرچه جرم کمتر باشد نسبت مولکولهای سریع در یک دمای معین بیشتر است. بنابراین احتمال اینکه هیدروژن در ارتفاعات زیاد از جو فرار کند بیشتر است، تا اکسیژن و ازت. کره ماه دارای جو رقیقی است. برای آنکه مولکولهای این جو احتمال زیادی برای فرار از کشش گرانشی ضعیف ماه ، حتی در دماهای پایین آنجا نداشته باشند، انتظار میرود که این مولکولها یا اتمها متعلق به عناصر سنگینتر باشند. طبق شواهدی ، در این جو گازهای بی اثر سنگین مانند کریپتون و گزنون وجود دارند که براثر واپاشی پرتوزا در تاریخ گذشته ماه تولید شدهاند. فشار جو ماه در حدود 10 برابر فشار جو زمین است.
توزیع ماکسولی
ماکسول قانون توزیع سرعتهای مولکولی را در سال 1859 میلادی به دست آورد. در آن زمان بررسی این قانون به کمک اندازه گیری مستقیم ممکن نبود و در حقیقت تا سال 1920 که اولین کوشش جدی در این راه توسط اشترن (Stern) به عمل آمد، هیچ اقدامی صورت نگرفته بود. افراد مختلفی تکنیکهای این کار را به سرعت بهبود بخشیدند. تا اینکه در سال 1955 یک بررسی تجربی بسیار دقیق در تائید این قانون (در مورد مولکولهای گاز توسط میلر (Miller) و کاش (Kusch) از دانشگاه کلمبیا صورت گرفت.
اسبابی که این دو نفر بکار بردند در مجموعهای از آزمایشها مقداری تالیوم در کوره قرار میدادند و دیوارههای کوره O را تا دمای یکنواخت 80±4K گرم کردند. در این دما تالیوم بخار میشود و با فشار 3.2x10-3 میلیمتر جیوه ، کوره را پر میکند. بعضی از مولکولهای بخار تالیوم از شکاف s به فضای کاملا تخلیه شده خارج کوره فرار میکند و روی استوانه چرخان R میافتند در این صورت استوانه که طولش L است تعدادی شیار به صورت مورب تعبیه شده که فقط یکی از آنها را میتوان دید. به ازای یک سرعت زاویهای معین استوانه (W) فقط مولکولهایی که دارای سرعت کاملا مشخص V هستند میتوانند بدون برخورد با دیوارهها از شیارها عبور کنند. سرعت V را میتوان از رابطه زیر بدست آورد:
V=LW/q و L/V= φ/W = زمان عبور مولکول از شیار
φ : تغییر مکان زاویهای بین ورودی و خروجی یک شیار مورب است. استوانه چرخان یک سرعت گزین است، سرعت انتخاب شده با سرعت زاویهای (قابل کنترل) W متناسب است.
نقص توزیع سرعت ماکسولی با نظریه جنبشی
اگرچه توزیع ماکسولی سرعت برای گازها در شرایط عادی سازگاری بسیار خوبی با مشاهدات دارد. ولی در چگالیهای بالا ، که فرضهای اساسی نظریه جنبشی کلاسیک صادق نیستند. این سازگاری نیز به هم میخورد. در این شرایط باید از توزیعهای سرعت مبتنی بر اصول مکانیک کوانتومی ، یعنی توزیع فرمی - دیراک (Fermi Dirac) بوز – انیشتین (Bose Einstein) استفاده کرد. این توزیعهای کوانتمی در ناحیه کلاسیک ( چگالی کم ) با توزیع ماکسولی توافق نزدیک دارند و در جایی که توزیع کلاسیک با شکست مواجه میشود با نتایج تجربی سازگارند. بنابراین در کاربرد توزیع ماکسولی محدودیتهایی وجود دارد. همانگونه که در واقع برای هر نظریهای چنین است.
يك روش محاسبه براي زاويه هاي خيلي كوچك اين است كه نسبت قوس را به شعاع حساب كنيم.
مثلا" براي زاويه 1 درجه داريم:(شكل 1)
و به همين ترتيب مي توان به دست آورد:
با توجه به شكل 2 داريم:
شكل2
BC را به اندازه ي خودش تا نقطه ي D امتداد مي دهيم و سپس D را به A وصل مي كنيم. در اين صورت دو مثلث مساوي ADC و ABC و زاويه BAD مساوي 30درجه به دست مي آيد. عمود BE را بر AD فرود مي آوريم ؛ مثلث قائم الزاويه BAE بازاويه 30 درجه(زاويه BAE ) به دست مي آيدو بنابراين =BE مي شود.
حال AE را از مثلث ABE طبق رابطه ي فيثاغورث به دست مي آوريم:
اگر به سه رقم اعشار اكتفا كرده باشيم ، اين عدد، همان عددي است كه در جدول ها براي 15 Sin ضبط شده است.
به اين ترتيب با اضافه كردن 016/ 0به سينوس 15 درجه به طور متوالي سينوس زاويه هاي 16، 17درجه و غيره به دست مي آيد:
براي اين منظور مي توان از قضيه ي فيثاغورث استفاده كرد.
فرض مي كنيم كه بخوا هيم سينوس زاويه 53 درجه را محاسبه كنيم:
بايد نسبت را به دست آوريم.(شكل3 )
شكل3
از طرفي داريم :
بنا بر اين: و لذا داريم :
دانشجو های عزیز:
سیمین بیات
امیر حسین حسین علی زاده
hossein i
900469434
سعیده علی پور
سمانه مویدی
مریم مشهدی
ارزو فتحی
زهرا کیانی
الناز انتظاری
سمن صبری
گزارش های شما به دستم رسید ولی به علت تکراری بودن در صفحه نمایش داده نمیشود.
قانون گازها و ستارگان
 با مطالعه و پژوهش در قوانین حاکم بر گازها می توان درک بهتر و وسیعتری نسبت به ساختار ابر سحابی ها و ستارگان و تحولات آنها داشت چرا که در تمام کائنات این تحولات هستند که باعث تشکیل ستارگان می شوند و سحابیها را به زایشگاه های کیهانی بدل کرده اند .
با مطالعه و پژوهش در قوانین حاکم بر گازها می توان درک بهتر و وسیعتری نسبت به ساختار ابر سحابی ها و ستارگان و تحولات آنها داشت چرا که در تمام کائنات این تحولات هستند که باعث تشکیل ستارگان می شوند و سحابیها را به زایشگاه های کیهانی بدل کرده اند .
در این نوشتار سعی بر آن خواهد شد تا قوانین حاکم بر گازها را در شرایط مختلف ترمودینامیکی مورد بررسی قرار داده و با زبانی ساده به چگونگی تاثیر آن در ستارگان پرداخته خواهد شد .
در ابتدا لازم است برای فهم بهتر مثال سیلندر وپیستون را در ذیل بیاوریم :
اگر سیلندری داشته باشیم که درون آن پر از گاز باشد و پیستون هم در بالای گازها و در قطر داخلی سیلندر قرار داشته باشد. حرارت گاز درون سیلندر به حرکت مولکولهای گاز وابسته است به آن معنی که اگر حرکت مولکولها زیاد(سریع) باشد گاز گرم ولی اگر حرکت مولکولها کند باشد گاز بطبع سرد خواهد بود .
از این پس گاز با شرایط بالا را در فرایندهای ترمودینامیکی مختلف بررسی می کنیم .
فرایند دما ثابت (ISO THERM) : اگر پیستون را به طرف پایین فشار دهیم حجم درون سیلندر کم می شود‚ ولی دما را ثابت نگه می داریم در این حال فشار افزایش می یابد چرا که با کاهش حجم فاصله بین مولکولها(فاصله آزاد) کم شده و برخورد بین مولکولی در حرکت مولکولها بیشتر شده و این امر افزایش فشار را باعث می شود که اگر فشارسنجی بر روی سیلندر نصب باشد صدق این مسئله را تایید می کند .
ثابت P1.V1 = P2 .V2 T = C

فرایند حجم ثابت (ISO VOLUME) : در این فرایند اگر حجم را ثابت نگه داشته یعنی پیستون را به بالا یا پایین حرکت ندهیم در اثر افزایش دما (دما در این فرایند متغیر است) باز هم سرعت مولکولها و بطبع برخورد های مولکولی بیشتر می شود که این امر نتیجه ای جز افزایش فشار را در بر ندارد و می توان توسط یک فشار سنج راستی پروسه را مشاهده کرد .
ثابت P1/P2 = T1/T2 V = C
( لازم به ذکر است علامت / در فرمول بالا نشان دهنده کسر است )

فرایند فشار ثابت (ISO BAR) : در این فرایند می توان یک سیلندر و پیستون را در نظر گرفت که در داخل سیلندر و در زیر پیستون مقداری گاز موجود است و بر روی پیستون مقداری وزنه قرار گرفته که در حالت اولیه بین وزن پیستون و وزنه های موجود بر روی پیستون و نیروی فشاری ناشی از وجود گاز در زیر پیستون تعادل برقرار است حال اگر به طور آهسته و با کندی حساب شده به گاز موجود درون سیلندر گرما دهیم و همچنین اجازه دهیم که پیستون آزادانه در سیلندر حرکت داشته باشد با گرماگیری گاز ‚ تمایل به افزایش فشار‚ در درون گاز افزایش می یابد ولی با تغییر مکان پیستون به سمت بالا و افزایش حجم گاز درون سیلندر‚ فشار ثابت خواهد ماند که به این تحول که تولید کننده کار نیز هست تحول فشار ثابت می گویند .
ثابت V1/V2 = T1/T2 P = C
(لازم به ذکر است علامت / در فرمول بالا نشان دهنده کسر است )

لازم به ذکر است در این تحول به دلیل اینکه دائما” حجم در حال افزایش است دما در ابتدای انبساط افزایش می یابد که خود عاملی برای انبساط است ولی در حین انبساط عمل افزایش حجم خود باعث کاهش دما خواهد شد .
وقتی ذخیره هیدروژنی ستاره کم شود ستاره انرژی کمتری نسبت به قبل تولید میکند و دیگر نمی تواند در برابر نیروی گرانش مقاومت کند. نیروی گرانش که حال خود به عنوان منبع انرژی جدیدی است باعث انقباض ستاره شده و جحم ستاره کاهش پیدا می کند (طبق قانون گازها) و ذرات به هم نزدیک تر شده و برخورد بیشتری باهم خواهند داشت که بر اثر همین مسئله هسته ستاره دوباره داغ شده و دما در ناحیه بیرونی هسته به اندازه ای می رسد که دوباره هیدروژن به هلیوم تبدیل شود . این قضیه پیامدهایی دارد و آن اینست که لایه های بیرونی ستاره منبسط شده و ستاره را به نسبت جرمی که دارد به غول یا ابر غول تبدیل میکند که دمای سطحی آن نیز کم و در حدود 3000 درجه کلوین است حال سوال دیگری که مطرح می شود اینست که چرا دمای سطحی اینگونه ستارگان کم می شود و در پاسخ باید گفت : اگر ستاره ای بسیار داغ باشد بطبع و طبق قانون حاکم بر گازها منبسط خواهد شد که بر اثر این انبساط و افزایش حجم در آن ستاره یک اثر سردی به وجود می آید که این سردی باعث کاهش داغی ستاره شده که خود می تواند به کاهش مصرف سوخت در درون ستاره بیانجامد .
ما می دانیم یک ابر سحابی( گازی ) که بر اثر نیروی گرانش متراکم می شود گرم هم می شود چرا که مقداری از انرژی پتانسیل درون خود را به انرژی جنبشی تبدیل کرده و این تبدیل انرژی باعث ازدیاد سرعت حرکتی مولکولهای ابر سحابی شده و تولید گرما می کند . دراین لحظه اگر جرم سحابی متراکم شده در حد معینی باشد که بتواند فشاری تولید کند که درخور و شایسته یک پیش ستاره و بعدها یک ستاره باشد کوره هسته ای در قلب سحابی متراکم شده که بعدها قلب یک ستاره خواهد بود روشن می شود و ترکیبات هسته ای در آن آغاز می شود که نتیجه آن تولید انرژی در گستره ای وسیع است.
ابرهای سحابی دارای چگالی برابر با0/1 تا 10 اتم در سانتی متر مکعب هستند و دمای آنها به طور متوسط حدود 170 درجه سانتیگراد است و با این شرایط و با حرکت سریع و سرگردانی که اتمها بعضا” دارند بعید به نظر می رسد که نیروی گرانش بتواند بر آنها اثر کرده و آنها را در کنار هم جمع کرده و تشکیل یک ناحیه چگال و متراکم دهد . پس باید درابر سحابی ها به دنبال مکانهایی با تراکم بیشتر (چگالی) بیشتر و دمای کمتر (سردتر) و همچنین نواحی تاریک بود چرا که در این مکانها اجتماع اتمها در هر سانتی متر بیشتر بوده و از طرفی حرکت اتمها به خاطر کمبود انرژی جنبشی نیز کند و کم است و نیروی گرانش (GRAVITY) بهتر می تواند آنها را تحت سیطره خود درآورده و تشکیل یک (گلوبول) دهد .(گلوبول سحابی کوچک متراکم و تاریکی است که می تواند یک پیش ستاره را به وجود آورد). دمای این قسمت ها به کمی بالاتر از صفرمطلق می رسد و البته این را باید ذکر کرد که این نواحی به این علت تاریکند که مقداری گرد و غبار نیز در خود داشته و این گرد و غبار جلوی نور ستارگان پشت سر خود را گرفته و اجازه رسیدن نور آنها را به ما نمی دهند که به صورت نواحی تیره رنگ در تصاویر تهیه شده از سحابیها مشخص شده اند .

به نواحی تیره در تصویر توجه کنید
در تشکیل یک ستاره عوامل متعددی وجود دارد که می تواند اختلالاتی در یک قسمت ابر سحابی به وجود آورده و آن را از دیگر قسمتها متمایز کند‚ یکی از این عوامل قرار گرفتن تحت تاثیر فشارهایی درونی است که قسمت متراکم را برای تشکیل یک پیش ستاره آماده میکند (که از طریق قانون گازها قابل توضیح است) که در بالا به آن اشاره شد و یکی از مهمترین علتها تحت تاثیر موج ضربه یک ابرنواختر قرار گرفتن است که باعث می شود جرم زیادی از گازها به یکباره در نقطه ای جمع شده و ناحیه ای متراکم را تشکیل دهد که با شرایط گفته شده در بالا می تواند به وجود آورنده یک پیش ستاره و در مرحله بعد یک ستاره باشد که قطر و جرم ستاره نیز به مقدار ماده تشکیل دهنده سحابی متراکم شده مربوط می شود .
نظریه جنبشی گازها
قوانین مکانیک را میتوان بطور آماری در دو سطح مختلف به مجموعهای از اتمها اعمال کرد در سطحی که نظریه جنبشی گازها نامیده میشود. به طریقی کم و بیش فیزیکی و با استفاده از روشهای نسبتا ساده میانگین گیری ریاضی ، عمل میکنیم. برای فهم نظریه جنبشی گاز را در فشار ، دما ، گرمای ویژه و انرژی داخلی این روش را که در سطح بکار برده میشود.
نگاه اجمالی
در ترمودینامیک فقط با متغیرهای ماکروسکوپیک ، مانند فشار و دما و حجم سر و کار داریم. قوانین اصلی ترمودینامیکها بر حسب چنین کمیتهایی بیان میشوند. ابدا درباره این امر که ماده از اتمها ساخته شده است صحبتی نمیکنند. لیکن مکانیک آماری ، که با همان حیطهای از علم سر و کار دارد که ترمودینامیک از آن بحث میکند و وجود اتمها را از پیش مفروض میداند. قوانین اصلی مکانیک آماری حامی قوانین مکانیکاند که در حدود اتمهای تشکیل دهنده سیسنم بکار میروند.
تاریخچه
نظریه جنبشی توسط رابرت بویل (Rabert Boyle) (1627 – 1691) ، دانیل بونولی (1700 – 1782) ، جیمز ژول (1818 – 1889) ، کرونیگ (1822 – 1874) ، رودولف کلاوسیوس (1822 – 1888) و کلرک ماکسول ( 1831 – 1879 ) و عدهای دیگر تکوین یافته است. در اینجا نظریه جنبشی را فقط در مورد گازها بکار میبریم، زیرا برهم کنشهای بین اتمها ، در گازها به مراتب متغیرترند تا در مایعات. و این امر مشکلات ریاضی را خیلی آسانتر میکند.
در سطح دیگر میتوان قوانین مکانیک را بطور آماری و با استفاده از روشهایی که صوریتر و انتزاعیتر از روشهای نظریه جنبشی هستند بکار برد. این رهیافت که توسط جی ویلارد گیبس (J.willard Gibbs) و لودویگ بولتز مانی (Ludwig Boltz manni) (1844 – 1906) و دیگران تکامل یافته است، مکانیک آماری نامیده میشود، که نظریه جنبشی را به عنوان یکی از شاخههای فرعی در بر میگیرد. با استفاده از این روشها میتوان قوانین ترمودینامیک را به دست آورد. بدین ترتیب معلوم میشود که ترمودینامیک شاخهای از علم مکانیک است.
محاسبه فشار بر پایه نظریه جنبشی
فشار یک گاز ایدهآل را با استفاده از نظریه جنبشی محاسبه میکنند. برای ساده کردن مطلب ، گازی را در یک ظرف مکعب شکل با دیوارههای کاملا کشسان در نظر میگیریم. فرض میکنیم طول هر ضلع مکعب L باشد. سطحهای عمود بر محور X را که مساحت هر کدام e2 است. A1 و A2 مینامیم. مولکولی را در نظر میگیریم که دارای سرعت V باشد. سرعت V را میتوان در راستای یالهای مولفههای Vx و Vy و Vz تجزیه کرد. اگر این ذره با A1 برخورد کند در بازگشت مولفه X سرعت آن معکوس می شود. این برخورد اثری رو ی مولفه Vy و یا Vy ندارد در نتیجه متغیر اندازه حرکت عبارت خواهد بود :
(m Vx - m Vx) = 2 m Vx - )= اندازه حرکت اولیه – اندازه حرکت نهایی
که بر A1 عمود است. بنابراین اندازه حرکتی e به A1 داده میشود برابر با m Vx2 خواهد بود زیرا اندازه حرکت کل پایسته است.
زمان لازم برای طی کردن مکعب برابر خواهد بود با Vx/L. در A2 دوباره مولفه y سرعت معکوس میشود و ذره به طرف A1 باز میگردد. با این فرض که در این میان برخوردی صورت نمیگیرد مدت رفت و برگشت برابر با 2 e Vx خواهد بود. به طوری که آهنگ انتقال اندازه حرکت از ذره به A1 عبارت است: mVx2/e = Vx/2e . 2 mVx ، برای به دست آوردن نیروی کل وارد بر سطح A1 ، یعنی آهنگ انتقال اندازه حرکتی از طرف تمام مولکولهای گاز به A1 داده میشود.
(P = M/e(Vx12 + Vx22 + Vx32
P = 1/2eV2
تعبیر دما از دیدگاه نظریه جنبشی
با توجه به فرمول RT 2/3 = 1/2 MV2 یعنی انرژی کل انتقال هر مول از مولکولهای یک گاز ایدهآل ، با دما متناسب است. میتوان گفت که این نتیجه با توجه به معادله بالا برای جور در آمدن نظریه جنبشی با معادله حالت یک گاز ایدهآل لازم است. و یا اینکه میتوان معادله بالا را به عنوان تعریفی از دما بر پایه نظریه جنبشی یا بر مبنای میکروسکوبیک در نظر گرفت. هر دو مورد بینشی از مفهوم دمای گاز به ما میدهد. دمای یک گاز مربوط است به انرژی جنبشی انتقال کل نسبت به مرکز جرم گاز اندازه گیری میشود. انرژی جنبشی مربوط به حرکت مرکز جرم گاز ربطی به دمای گاز ندارد.
حرکت کاتورهای را به عنوان بخشی از تعریف آماری یک گاز ایدهآل در نظر گرفت. V2 را بر این اساس میتوان محاسبه کرد. در یک توزیع کاتورهای سرعتهای مولکولی ، مرکز جرم در حال سکون خواهد بود. بنابراین ما باید چارچوب مرجعی را بکار ببریم که در آن مرکز جرم گاز در حال سکون باشد. در چارچوبهای دیگر ، سرعت هر یک از مولکولها به اندازه U (سرعت مرکز جرم در آن چارچوب) از سرعت آنها در چارچوب مرکز جرم بیشتر است. در اینصورت حرکتها دیگر کترهای نخواهد بود و برای V2 مقادیر متفاوتی بدست میآید. پس دمای گاز داخل یک ظرف در یک قطار متحرک افزایش مییابد. میدانیم که M V2 1/2 میانگین انرژی جنبشی انتقالی هر مولکول است. این کمیت در یک دمای معین که در این مورد صفر درجه سلسیوس است، برای همه گازها مقدار تقریبا یکسانی دارد. پس نتیجه میگیریم که در دمای T ، نسبت جذر میانگین مربعی سرعتهای مولکولهای دو گاز مختلف مساوی است با ریشه دمای عکس نسبت به مربعهای آنها.
T=2/3k m1 V12/2= 2/3k m2 V22/2
مسافت آزاد میانگین
در فاصله برخوردهای پیدرپی ، هر مولکول از گاز با سرعت ثابتی در طول یک خط راست حرکت میکند. فاصله متوسط بین این برخوردهای پیدرپی را مسافت آزاد میانگین مینامند. اگر مولکولها به شکل نقطه بودند، اصلا با هم برخورد نمیکردند. و مسافت آزاد میانگین بینهایت میشد. اما مولکولها نقطهای نیستند و بدین جهت برخوردهایی روی میدهد. اگر تعداد مولکولها آنقدر زیاد بود که میتوانستند فضایی را که در اختیار دارند کاملا پر کنند و دیگر جایی برای حرکت انتقالی آنها باقی نمیماند. آن وقت مسافت آزاد میانگین صفر میشد. بنابراین مسافت آزاد میانگین بستگی دارد به اندازه مولکولها و تعداد واحد آنها در واحد حجم. و به قطر d و مولکولهای گاز به صورت کروی هستند در این صورت مقطع برای برخورد برابر با лd2 خواهد بود.
مولکولی با قطر 2d را در نظر میگیریم که با سرعت V در داخل گازی از ذرات نقطهای هم ارز حرکت میکند. این مولکول در مدت t استوانهای با سطح مقطع лd2 و طول Vt را میروبد. اگر nv تعداد مولکولها در واحد حجم باشد استوانه شامل (лd2 Vt ) nv ذره خواهد بود. مسافت آزاد میانگین ، L ، فاصله متوسط بین دو برخورد پیدرپی است بنابراین ، L ، عبارت است از کل مسافتی که مولکول در مدت t میپیماید. (Vt) تقسیم بر تعداد برخوردهایی که در این مدت انجام میدهد. یعنی
I = Vt/πd2nv =1/√2πnd2
I=1/√2πnd2
این میانگین بر مبنای تصویری است که در آن یک مولکول با هدفهای ساکن برخورد میکند. در واقع ، برخوردهای مولکول با هدف دمای متحرک انجام میگیرد در نتیجه تعداد برخورد دما از این مقدار بیشتر است.
توزیع سرعتهای مولکولی
با توجه به سرعت جذر میانگین مربعی مولکولهای گاز ، اما گستره سرعتهای تکتک مولکولها بسیار وسیع است. بطوری که برای هر گازی منحنیای از سرعتها مولکولی وجود دارد که به دما وابسته است. اگر سرعتهای تمام مولکولهای یک گاز یکسان باشند این وضعیت نمیتواند مدت زیاد دوام بیاورد. زیرا سرعتهای مولکولی به علت برخوردها تغییر خواهند کرد. با وجود این انتظار نداریم که سرعت تعداد زیادی از مولکولها بسیار کمتر از Vrms (یعنی نزدیک صفر) یا بسیار بیشتر از Vrms ، زیرا وجود چنین سرعتهایی مستلزم آن است که یک رشته برخوردهایی نامحتمل و موجی صورت بگیرد. مسئله محتملترین توزیع سرعتها در مورد تعداد زیادی از مولکولهای یک گاز را ابتدا کلوک ماکسول حل کرد. قانونی که او ارائه کرد در مورد نمونهای از گاز که N مولکول را شامل میشد چنین است :
N(V)=4πN(m/2πKt)3/2V2e-mv2/2kt
در این معادله N(V)dV تعداد مولکولهایی است که سرعت بین V و V+3v است، T دمای مطلق ، K ثابت بولتزمن ، m جرم هر مولکول است. تعداد کل مولکولهای گاز (N) را ، با جمع کردن (یعنی انتگرالگیری) تعداد موجود در هر بازه دیفرانسیلی سرعت از صفر تا بینهایت به دست میآید. واحد (N(V میتواند مثلا مولکول برا سانتیمتر بر ثانیه باشد.
N =∫∞0N(V)dv
توزیع سرعتهای مولکولی در مایعات
توزیع سرعتهای مولکولی در مایعات شبیه گاز است. اما بعضی از مولکولهای مایع (آنهایی که سریعترند) میتوانند در دماهایی کاملا پایینتر از نقطه جوش عادی از سطح مایع بگریزند. (یعنی تبخیر شوند). فقط این مولکولها هستند که میتوانند بر جاذبه مولکولهای سطح فائق آیند. و در اثر تبخیر فرار کنند. بنابراین انرژی جنبشی میانگین مولکولهای باقیمانده نیز کاهش مییابد در نتیجه دمای مایع پایین میآید. این امر روشن میکند که چرا تبخیر فرایند سرمایشی است.
مثال واقعی در مورد توزیع سرعتهای مولکولی
با توجه به فرمول N(V)= Σ410N(M/2πkT)3/2 توزیع سرعتهای مولکولی هم به جرم مولکول و هم به دما بستگی دارد هرچه جرم کمتر باشد نسبت مولکولهای سریع در یک دمای معین بیشتر است. بنابراین احتمال اینکه هیدروژن در ارتفاعات زیاد از جو فرار کند بیشتر است، تا اکسیژن و ازت. کره ماه دارای جو رقیقی است. برای آنکه مولکولهای این جو احتمال زیادی برای فرار از کشش گرانشی ضعیف ماه ، حتی در دماهای پایین آنجا نداشته باشند، انتظار میرود که این مولکولها یا اتمها متعلق به عناصر سنگینتر باشند. طبق شواهدی ، در این جو گازهای بی اثر سنگین مانند کریپتون و گزنون وجود دارند که براثر واپاشی پرتوزا در تاریخ گذشته ماه تولید شدهاند. فشار جو ماه در حدود 10 برابر فشار جو زمین است.
توزیع ماکسولی
ماکسول قانون توزیع سرعتهای مولکولی را در سال 1859 میلادی به دست آورد. در آن زمان بررسی این قانون به کمک اندازه گیری مستقیم ممکن نبود و در حقیقت تا سال 1920 که اولین کوشش جدی در این راه توسط اشترن (Stern) به عمل آمد، هیچ اقدامی صورت نگرفته بود. افراد مختلفی تکنیکهای این کار را به سرعت بهبود بخشیدند. تا اینکه در سال 1955 یک بررسی تجربی بسیار دقیق در تائید این قانون (در مورد مولکولهای گاز توسط میلر (Miller) و کاش (Kusch) از دانشگاه کلمبیا صورت گرفت.
اسبابی که این دو نفر بکار بردند در مجموعهای از آزمایشها مقداری تالیوم در کوره قرار میدادند و دیوارههای کوره O را تا دمای یکنواخت 80±4K گرم کردند. در این دما تالیوم بخار میشود و با فشار 3.2x10-3 میلیمتر جیوه ، کوره را پر میکند. بعضی از مولکولهای بخار تالیوم از شکاف s به فضای کاملا تخلیه شده خارج کوره فرار میکند و روی استوانه چرخان R میافتند در این صورت استوانه که طولش L است تعدادی شیار به صورت مورب تعبیه شده که فقط یکی از آنها را میتوان دید. به ازای یک سرعت زاویهای معین استوانه (W) فقط مولکولهایی که دارای سرعت کاملا مشخص V هستند میتوانند بدون برخورد با دیوارهها از شیارها عبور کنند. سرعت V را میتوان از رابطه زیر بدست آورد:
V=LW/q و L/V= φ/W = زمان عبور مولکول از شیار
φ : تغییر مکان زاویهای بین ورودی و خروجی یک شیار مورب است. استوانه چرخان یک سرعت گزین است، سرعت انتخاب شده با سرعت زاویهای (قابل کنترل) W متناسب است.
نقص توزیع سرعت ماکسولی با نظریه جنبشی
اگرچه توزیع ماکسولی سرعت برای گازها در شرایط عادی سازگاری بسیار خوبی با مشاهدات دارد. ولی در چگالیهای بالا ، که فرضهای اساسی نظریه جنبشی کلاسیک صادق نیستند. این سازگاری نیز به هم میخورد. در این شرایط باید از توزیعهای سرعت مبتنی بر اصول مکانیک کوانتومی ، یعنی توزیع فرمی - دیراک (Fermi Dirac) بوز – انیشتین (Bose Einstein) استفاده کرد. این توزیعهای کوانتمی در ناحیه کلاسیک ( چگالی کم ) با توزیع ماکسولی توافق نزدیک دارند و در جایی که توزیع کلاسیک با شکست مواجه میشود با نتایج تجربی سازگارند. بنابراین در کاربرد توزیع ماکسولی محدودیتهایی وجود دارد. همانگونه که در واقع برای هر نظریهای چنین است.
قوانین گازها
|
قوانين گازها
جهت آشنائي با تحولاتي كه در سيستمهاي تراكم به وقوع مي پيوندد، تغييرات فشار، دما و حجمگازهاي ايده آل تحت تحولات مختلف مورد بررسي قرار مي گيرد.
الف:قانون چارلز
تحت فشار ثابت ، باگرم كردن گازها حجم آن افزايش و با سرد كردن گاز حجم آن كاهش مي يابد. بطوريكه:
(T1/T2)p=(V1/V2)p
كه درآن Pفشار مطلق، Tدماي مطلق و Vحجم گاز مي باشد. اين تراكم را اصطلاحا تك فشار(Isobar) مي نامند. انديس p در بيرون پرانتز مبين ثابت بودن فشار مي باشد.
ب:قانون بويل
تحت دماي ثابت، با افزايش فشار (تراكم) حجم گاز كاهش و باكاهش فشار(انبساط ) حجم آن افزايش مي يابد. اين تحول را تك دما (Isothermal) مي نامند.
(P1/P2)r=(V2/V1)r
ج:قانون آمونتون
تحت حجم ثابت، با افزايش فشار ، دماي گاز افزايش يافته و باكاهش فشار دماي آن كاهش مي يابد.
(P1/P2)v=(T1/T2)v
قانون كلي گازهاي ايده آل
باتركيب روابط فوق مي توان در حالت كلي، تغييرات فشار، دما و حجم گازها رادر صورت تغييرحداقل يكي از سه عامل فوق از رابطه بدست آورد.
P1V1/T1=P2V2/T2
قانون گازهاي كامل
بين حجم،دما و فشار گازهاي كامل همواره يك رابطه برقرار بوده كه با رابطه ذیل نشان داده شده است:
PV =MRT
كه درآن P فشار مطلق، V حجم ، M جرم مولكولي گاز ،R ضريب ثابت گاز و T دماي مطلق مي باشد.
|
همان وقت که اسحاق نيوتن در کمبريج درباره نور و جاذبه ميانديشيد، يک نفر انگليسي ديگر به نام رابرت بويل ، در آکسفورد سرگرم مطالعه در باب خواص مکانيکي و تراکم پذيري هوا و ساير گازها بود. بويل که خبر اختراع گلوله سربي اوتوفون گريکه را شنيده بود، طرح خويش را تکميل کرد، و دست به کار آزمايشهايي براي اندازه گيري حجم هوا در فشار کم و زياد شدنتيجه کارهاي وي چيزي است که اکنون به قانون بويل ماريوت معروف است، و بيان ميکند که حجم مقدار معيني از هر گاز در دماي معين با فشاري که بر آن گاز وارد ميشود، بطور معکوس ، متناسب است با فشاري که بر آن گاز وارد ميشود
حدود يک قرن بعد ، ژوزف گيلوساک فرانسوي ، در ضمن مطالعه انبساط گازها ، قانون مهم ديگري پيدا کرد که بيان آن اين است: فشار هر گاز محتوي در حجم معين به ازاي هر يک درجه سانتيگراد افزايش دما ، به اندازه 273/1 حجم اوليهاش افزايش مييابد. همين قانون را يک فرانسوي ديگر به نام ژاک شارل ، دو سال پيش از آن کشف کرده بود. و از اين رو اغلب آن را قانون شارل گيلوساک مينامند. اين دو قانون مبناي ساخت دماسنجهاي گازي قرار گرفت.
دماسنج مایعی :
اين نوع دماسنج يکي از رايج ترين انواع دماسنجهاي مورد استفاده در صنعت و غيره مي- باشد. عمدتا اين نوع دماسنج را بعنوان دماسنجهاي جيوه اي يا الکلي مي شناسيم. ساختمان اين نوع دماسنجها از يک مخزن مايع و يک لوله مويين تشکيل شده که مايع درون مخزن در اثر انبساط از لوله مويين بالا رفته و دماي متناسب را نشان ميدهد.دماسنج جيوه اي را مي توان براي اندازگيري دما از 37.8- تا315 سانتي گراد استفاده نمود. اما اگرفضاي بالاي سطح جيوه را از گاز ازت پر نمايند ، مي توان تا دماي 538 درجه از آن استفاده نمود.
دماسنج انبساط سیال:
اين نوع دماسنج يکي از باصرفه ترين ، رايج ترين و تطبيق پذير ترين وسايل اندازگيري دما در صنعت مي باشد.اساس کار اين دماسنج در شکل مقابل نشان داده شده است.همانگونه که ملاحظه مي شود با افزايش دما فشار درون حباب که مي تواند محتوي مايع ، گاز يا بخار باشد ، بالا رفته و توسط فشار سنج اندازه گيري مي شود. طول لوله مويين مي تواند تا 60 متر باشد ؛ اما اين مقدار بر دقت اندازه گيري دما تاثير گذار خواهد بود.بهترين حالت زماني است
دماسنجهای الکتریکی:
اين نوع دماسنجها اصولا کاربردهاي فراواني در صنعت داشته و قادرند از دماهاي پايين تا دماهاي بسيار بالا را اندازه گيري نمايند.که عمدتا بصورت مقاومتي و ترموکوپل هستند.
دماسنج با مقاومت الکتريکي:
دماسنج مقاومتي به صورت يک سيم بلند و ظريف است، معمولا آن را به دور يک قاب نازک ميپيچند تا از فشار ناشي از تغيير طول سيم که در اثر انقباض آن در موقع سرد شدن پيش ميآيد، جلوگيري کند. در شرايط ويژه ميتوان سيم را به دور جسمي که منظور اندازه گيري دماي آن است پيچيد يا در داخل آن قرار داد. در گستره دماي خيلي پايين ، ( دماسنجهاي مقاومتي معمولا از مقاومتهاي کوچک راديويي باترکيب کربن يا بلور ژرمانيوم که ناخالصي آن آرسنيک است و جسم حاصل در درون يک کپسول مسدود شده پر از هليوم قرار دارد، تشکيل ميشوند. اين دماسنج را ميتوان بر روي سطح جسمي که منظور اندازه گيري دماي آن است سوار کرد يا در حفرهاي که براي اين منظور ايجاد شده است، قرار داد. دماسنج مقاومتي پلاتين را ميتوان براي کارهاي خيلي دقيق در گستره –253 تا 1200 درجه سانتيگراد به کار برد.
ترميستور:
ترميستور يک وسيله نيمه رساناست که برخلاف فلزات ، داراي ضريب دماي مقاومت منفي است . بعلاوه مقاومت آن بصورت نمايي با دما تغيير مي کند. ترميستور يک وسطله بسيار حساس است و انتظار مي رود که با درجه بندي مناسب ، داراي عملکرد ثابتي تا 0.01 سانتي گراد باشد.يکي از ويژگي هاي جالب آن اينستکه مي توان از آن بعنوان جبران کننده دماي مدار هاي الکتريکي استفاده نمود.
دماسنج کریستال کوارتز:
يک روش جديد و بسيار دقيق اندازه گيري دما بر مبناي حساسيت فرکانس تشديد کريستال کوارتز به تغيير دما استوار است .وقتي از زاويه برش مناسب براي کريستال استفاد شود، يک تطابق کاملا خطي ميان فرکانس و دما برقرار ميگردد. مدلهاي تجاري اين وسيله از شمارنده هاي الکترونيکي و دستگاه قرائت رقم نما براي اندازه گيري فرکانس استفاده مي کنند. با اين وسيله تا حساسيت 0.001 C ادعا شده است.گستره دمايي کار کرد اين دستگاه از منفي 40 درجه تا 230 درجه سانتي گراد ادعا شده است.
دمانگاری کریستال مایع:
کريستالهاي مايع خميري ، که از استرهاي کلسترول ساخته شده اند پاسخ جالبي به دما از خود نشان مي دهند . در يک گستره تکرار پذير دما ، کريستال مايع همه رنگهاي طيف رنگي را از خود آشکار مي سازد.اين پديده بازگشت پذير و تکرار پذير است . با تغيير دادن فرمول موردنظر مي توان ازکريستالهاي مايع ازکمترازصفردرجه تا چندصددرجه سانتي گراداستفاده نمود.
ترموکوپل:
ترموکوپل وسيله ديگري است که براي اندازه گيري دما مورد استفاده قرار ميگيرد. در اين نوع دماسنج از خاصيت انبساط و انقباض اجسام جامد استفاده ميگردد. گستره يک ترموکوپل بستگي به موادي دارد که ترموکوپل از آن ساخته شده است. گستره يک ترموکوپل پلاتنيوم ـ ايروديوم که 10 درصد پلاتينيوم دارد از صفر تا C 1600 است. مزيت ترموکوپل در اين است که بخاطر جرم کوچک ، خيلي سريع با سيستمي که اندازه گيري دماي آن مورد نظر است، به حال تعادل گرمايي در ميآيد. لذا تغييرات دما به آساني بر آن اثر ميکند، ولي دقت دماسنج مقاومتي پلاتين را ندارد.
برتري دماسنج ترموكوپل:
برای اندازه گیری دماهای بالا تا حدود 1500 نيز ميتوان از آن استفاده كرد.
براي اندازهگيري اختلاف دماهاي بسيار كوچك حدود 001/0 درجه سانتيگراد نيز به كار
آذزسنج:
ااين نوع دماسنج که به آن دماسنج غير تماسي هم گفته مي شود ، بر پايه رنگ نور انتشار يافته از جسم بوده که در نهايت دماي جسم مورد نظر را اندازه گري مي کند. براساس اين حقيقت که تمامي اجسام سياه يک اندازه دمايي را نشان خواهند داد ، نتيجه ميگيريم که دامنه کاربردي اين نوع دماسنج در دماهاي بالاي سرخ بوده و براي آهن تقريبا بالاي 500 درجه سانتي گراد مي باشد.
طرز کار:
نور ايجاد شده توسط جسم از درون يک سيستم اپتيکال (با بزرگ نمايي معين) که در درون آن يک لامپ گداخته کوچک فرار داده شده ، گذرانده مي شود . (بدين ترتيب اگر کسي از درون چشمي بدرون اين سيستم نگاه مي کند ، نوري بسيار باريکي را ملاحظه خواهد کرد.) در برخورد اين نور با فيلمان لامپ ، جرياني را از فيلمان عبور خواهد داد که تعيين کننده ميزان دماي جسم است. اين جريان توسط پتانسيومتري که بين منبع تغذيه (يک باطري) و لامپ قرار داده شده کنترل ميگردد. براي نمايش دما از يک آم متر (ammeter ) استفاده ميگردد. دامنه آم متر از 900F براي دماي 500 درجه سانتي گراد تا 3000F براي دماي 1600 درجه سانتي گراد متغيير است.
دماسنج کامپیوترها:
برای آگاهی از وضعیت کارکرد ودمای درایو هاوcpuکامپیمتر شخصی دستگاهی با نام"Remote Panel Multifunction"ساخته شده و میتواند15خروجی کنترلی بیرون دهد.
*دماسنج . رطوبت سنج حداقل/حداکثر دیجیتال
1-مدل parpex 40
در این مدل استفاده کننده حداکثر دمای قابل قبول برای گلخانه را به دستگاه میدهد.دستگاه علاوه بر نمایش دما هر گاه دمای محیط بیش از مقدار تعیین شده باشد یک رله را فعال میکند .کنتاکتهای این رله میتوانند مستقیما یا با واسطه سیستمهای خنک کننده مانند فن و ... را فعال کرده و باعث کم شدن دما میشوند.همینکه دما کاهش پیدا کرد بطور اتوماتیک فن و... خاموش میشوند.محدوده دما از 5 درجه تا 70 درجه قابل تنظیهمان طور که ملاحظه میشود این دستگاه قادر است دمای گلخانه را زیر دمای دلخواه استفاده کننده مثلا 30 درجه سانتیگراد نگه دارد.محدوده دما از 5 درجه تا 70 درجه قابل تنظیم است.
2-مدل parpex 45 .
در این مدل استفاده کننده حداقل و حداکثر دمای قابل قبول برای گلخانه را به دستگاه میدهد.دستگاه علاوه بر نمایش دما هر گاه دمای محیط بیش از مقدار تعیین شده باشد یک رله را فعال میکند .کنتاکتهای این رله میتوانند مستقیما یا با واسطه سیستمهای خنک کننده مانند فن و ... را فعال کرده و باعث کم شدن دما میشوند.همینکه دما کاهش پیدا کرد بطور اتوماتیک فن و... خاموش میشوند.همچنین
هر گاه دمای محیط کمتر از مقدار تعیین شده شود یک رله دیگر فعال میشود .کنتاکتهای این رله میتوانند مستقیما یا با واسطه سیستمهای گرم کننده مانند هیتر و ... را فعال کرده و باعث زیاد شدن دما بشوند.همینکه دما افزایش پیدا کرد بطور اتوماتیک هیتر و... خاموش میشوند.
همان طور که ملاحظه میشود این دستگاه قادر است دمای گلخانه را بین دو دمای دلخواه استفاده کننده مثلا بین 15 درجه تا 30 درجه سانتیگراد نگه دارد.محدوده دما از 5 درجه تا 70 درجه قابل تنظیم است.
3-مدل parpex 50
در این مدل استفاده کننده حداکثر رطوبت نسبی قابل قبول برای گلخانه را به دستگاه میدهد.دستگاه علاوه بر نمایش رطوبت نسبی هر گاه رطوبت نسبی محیط بیش از مقدار تعیین شده باشد یک رله را فعال میکند .کنتاکتهای این رله میتوانند مستقیما یا با واسطه سیستمهای کم کننده رطوبت مانند فن و ... را فعال کرده و باعث کم شدن رطوبت نسبی میشوند.همینکه رطوبت نسبی کاهش پیدا کرد بطور اتوماتیک فن و... خاموش میشوند.ان طور که ملاحظه میشود این دستگاه قادر است رطوبت گلخانه را زیر رطوبت دلخواه استفاده کننده مثلا 40% نگه دارد. محدوده نتظیم رطوبت نسبی از 10% تا 90% میباشد.
4-مدل parpex 55
در این مدل استفاده کننده حداقل و حداکثر رطوبت نسبی قابل قبول برای گلخانه را به دستگاه میدهد.دستگاه علاوه بر نمایش رطوبت محیط هر گاه رطوبت نسبی محیط بیش از مقدار تعیین شده باشد یک رله را فعال میکند .کنتاکتهای این رله میتوانند مستقیما یا با واسطه سیستمهای کاهشدهنده رطوبت مانند فن و ... را فعال کرده و باعث کم شدن رطوبت میشوند.همینکه رطوبت کاهش پیدا کرد بطور اتوماتیک فن و... خاموش میشوند.همچنین
هر گاه رطوبت محیط کمتر از مقدار تعیین شده شود یک رله دیگر فعال میشود .کنتاکتهای این رله میتوانند مستقیما یا با واسطه سیستمهای تولید رطوبت مانند دستگاهاهی رطوبت ساز و ... را فعال کرده و باعث زیاد شدن رطوبت بشوند.همینکه رطوبت افزایش پیدا کرد بطور اتوماتیک دستگاه های رطوبت ساز و... خاموش میشوند.
همان طور که ملاحظه میشود این دستگاه قادر است رطوبت نسبی گلخانه را بین دو رطوبت دلخواه استفاده کننده مثلا بین 10% تا 50 درجه نگه دارد.محدوده نتظیم رطوبت نسبی از 10% تا 90% میباشد.
*چرا در دماسنج جیوه ریخته اند؟
واژه ی دماسنج خود به شما می گوید كه چه كاری از دستش بر می آید.
دما یعنی حرارت و سنج یعنی اندازه گرفتن آن. پس دماسنج دستگاهی است كه با آن درجه حرارت را تعیین می كنند. برای تعیین حرارت، تنها راه، این است كه اثر و تغییرات آن را بر جسمی مورد توجه قرار دهیم. مثلاً چون ما تغییر محسوسی، بر اثر حرارت، در جسمی مشـاهده كنیم. درباره اش می گوییم: « این جسم خیلی داغ است! »
گرما و سرما، اجسام بسیاری را تحت تأثیر و دگرگونی قرار می دهند. پس ما برای درست كردن دماسنج به ماده ای نیازمندیم كه سرما و گرما در آن بی تأثیر بوده، حالت طبیعی اش را دگرگون نسازد. برای این منظور، جیوه مناسب ترین ماده است
هر چند كه حرارت باعث افزایش حجم جیوه می شود، ولی درجه ی این افزایش در همه ی حالات ثابت و معین است. مثلاً هر گاه جیوه ای را در یك لوله ی شیشه ای بریزیم و آن را گرم كنیم، خواهیم دید كه جیوه تا حد معینی انبساط یافته، خود به خود در لوله بالا می آید. سپس هر گاه مجدداً عین همان حرارت را به جیوه بدهیم دوباره تا همان نقطه ی اول بالا خواهد آمد. پس دماسنج به سادگی از یك لوله ی شیشه ای حاوی جیوه درست می شود. البته باید آن لوله را با اعداد درجه بندی هم بكنیم تا بتواند درجه بالا و پائین آمدن جیوه را به روشنی بیان كند.
در دماسنج های جدید، جیوه در لوله ای به باریكی یك سنجاق ریخته شده و منفذ آن نیز از موی انسان تنگ تر است. در انتهای لوله، مخزن كوچكی است كه فقط در آن، به اندازه ی لازم جیوه قرار دارد. اما در خود لوله به جای جیوه، یا گاز نیتروژن ریخته اند و یا اصلاً هوایش را كشیده و خلأ در آن ایجـاد كرده اند. جیوه در چنین لوله ای بالا و پایین می رود و بدین وسیله درجه حرارت را تعیین می كند
بر اثر گرما حجم جیوه افزایش می یابد = انبساط جیوه
بر اثر سرما حجم جیوه كاهش می یابد = انقباض جیوه
*دو شیوه در درجه بندی لوله دماسنج متداول است:
1 - فارنهایت 2 - صد بخشی یا سانتیگراد
در درجه بندی صد بخشی، صفر، نقطه ی انجماد آب است و 100 نقطه جوش آن. اما در درجه بندی فارنهایت، 32، نقطه ی انجماد است و 212 نقطه ی جوش آن.
دماسنج پزشكی كه برای تعیین درجه ی حرارت بدن ما به كار می رود، به گونه ای ساخته شده كه وقتی جیوه در لوله، بالا رفت تا مدتی همچنان بر سر جایش باقی می ماند. سپس باید آن را به شدت تكان بدهیم تا جیوه، دگر باره به مخزن خود باز گردد.
*دماسنج دیجیتال با نمایشگر کریستال مایع:
در این مدار آی سی ICL7136 به کار گرفته شده است که ولتاژ رسیده از دیود حسگر حرارت را را اندازه گیری می نماید.برای نمایش اطلاعات از یک نمایشگر کریستال مایع 3/5 رقم به شماره SP521PR استفاده شده است. که با ارزش ترین رقم آن تنها امکان نمایش عدد یک را دارد. در صورت نیاز می توانید با کمی تغییر در مدار از نمایشگرهای ال ای دی و نظیر آنها نیز استفاده نمایید. انرژی مصرفی آی سی ICL7136 بسیار اندک بوده به گونه ای که دماسنج دیجیتال شما می تواند حدود 3 ماه به صورت پیوسته تنها با یک باتری 9 ولت به خوبی دمای محیط را اندازه گیری نماید. توجه داشته باشد که برای آیسی و نمایشگر مدار حتماً از سوکت استفاده مایید.
تنظیم و راه اندازی :
پس از ساخت مدار ، هنگامی که مطمئن شدید همه چیز به درستی انجام شده است ، تغذیه مدار را متصل نمایید. دماسنج دیجیتال شما قبل از استفاده نیاز به تنظیم دارد. معمولاً این تنظیم را در دمای صفر و 100 درجه انجام داده و ملاک را مخلوط آب و یخ برای صفر درجه و آب جوش برای 100 درجه قرار می دهند.
برای تنظیم ابتدا سنسور را در مخلوط آب و یخ قرار داده و توسط پتانسیومتر VR2 دما را بر روی صفر درجه تنظیم نمایید. پس از آن سنسور را در آب در حال جوشیدن قرار داده و پتانسیومتر VR1 را آنقدر بچرخانید تا دماسنج دیجیتال عدد 100 را نمایش دهد. حال دستگاه شما تنظیم شده و آماده به کار است.
قانون بویل
قانون بویل قانونی در علم شیمی است که بیان میکند حجمگازها با وارد شدن فشار به طور منظمی کاهش می یابد؛ به عبارت دیگر، در گازها همواره میان حجم و فشار رابطه ای وارونه وجود دارد. این قانون را دانشمند انگلیسی، رابرت بویل (۱۶۲۷-۱۶۹۱) کشف کرده است.
که در آن
- p نشان دهنده فشار
- v نشان دهنده حجم
- و k نشان دهنده مقدار ثابت است.
قانون بویل به این صورت نیز بیان شده است:
-
-
- که در آن
 فشار گاز ایدهآل در قبل از فرآیند
فشار گاز ایدهآل در قبل از فرآیند حجم گاز ایدهآل در قبل از فرآیند
حجم گاز ایدهآل در قبل از فرآیند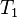 دمای گاز ایدهآل در قبل از فرآیند
دمای گاز ایدهآل در قبل از فرآیند فشار گاز ایدهآل در بعد از فرآیند
فشار گاز ایدهآل در بعد از فرآیند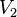 حجم گاز ایدهآل در بعد از فرآیند
حجم گاز ایدهآل در بعد از فرآیند دمای گاز ایدهآل در بعد از فرآیند
دمای گاز ایدهآل در بعد از فرآیند
-

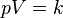
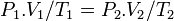
 آمار
وب سایت:
آمار
وب سایت:

